Seminar 6: Naive Bayes Classifier
여러분이 HW5의 과제를 열심히 했다면, 자연어 데이터를 전처리하는 방법 중 하나인 “토큰화(tokenization)”을 잘 이해했을 것이다 👏
이번 포스트에서는 실제 데이터에서 토큰화를 적용하고, 간단한 ML 모델을 만들어보겠다.
Spam Classifier
SNS Spam Collection Dataset에는 5천개 정도의 이메일 데이터가 있다.
v1 v2
0 ham Go until jurong point, crazy.. Available only ...
1 ham Ok lar... Joking wif u oni...
2 spam Free entry in 2 a wkly comp to win FA Cup fina...
3 ham U dun say so early hor... U c already then say...
4 ham Nah I don't think he goes to usf, he lives aro...
메일 본문과 함께 스팸(spam) 메일과 일반(ham) 메일로 레이블이 있는데, 이 데이터으로 스팸인지 아닌지 분류하는 간단한 분류기를 구현해보겠다.
Naive Bayes Classifier
데이터를 서로 다른 레이블로 분류하는 문제를 푸는 classifier에는 여러가지 종류가 있다.
- Logistic Regression
- KNN Classifier
- Naive Bayes Classifier
- Decision-tree based classifiers…
이번 포스트에서는 그 중에서 <Naive Bayes classifier>라는 분류기를 직접 구현해볼 것이다.
이론
먼저 Naive Bayes의 이론을 하나씩 살펴보자.
NB의 목표는 $p(c_k \mid x)$의 조건부 확률을 구하는 것이다. 이 확률은 데이터 $x$가 주어졌을 때 레이블 $c_k$일 확률을 말한다. 좀더 풀어쓰면…
- $p(S = T \mid x)$: 데이터 $x$가 스팸(spam)일 확률
- $p(S = F \mid x)$: 데이터 $x$가 햄(ham)일 확률
그런데 위와 같은 조건부 확률은 베이즈 정리(Bayes Theorem)에 의해 아래와 같이 풀어 쓸 수 있다.
\[p(c_k \mid x) = \frac{p(c_k) \cdot p(x \mid c_k)}{p(x)}\]분모 형태에서 각 확률의 의미를 살펴보면
- $p(c_k)$: 레이블이 $c_k$일 확률
- $p(S=T)$: 스팸 메일일 확률 = (스팸 메일의 수) / (전체 메일의 수)
- $p(x \mid c_k)$: 레이블이 $c_k$일 때, 데이터 $x$가 등장할 확률
- $p(x)$: 데이터 $x$가 등장할 확률
이때 $p(x)$는 생각할 필요가 없는게, 정확한 값을 구할 수 없기 때문이다. 우리가 지금 보는 스팸 메일 분류 문제라면, 데이터 $x$는 "Go until jurong point, crazy.."라는 메일 본문에 해당하는데, 이 메일 본문은 아주 거대한 코퍼스 공간 위의 한 점에 불과하기 때문에 확률이 정말 낮다.
물론 확률을 정의하는 전체 공간을 명확히 정의하면 실제 $p(x)$의 값을 구할 수도 있을 것이다. 그러나 지금 우리가 다루는 문제에서는 $p(x)$ 값을 아는 것이 전혀 의미가 없다.
일단 우리는 $p(c_k \mid x)$의 값이 큰 레이블을 정답으로 여길 것이다. 그래서
\[y = \underset{c_k}{\text{argmax}} \; p(c_k \mid x)\]을 구하게 되는데, $p(S =T \mid x)$에서나 $p(S = F \mid x)$에서나 $p(x)$는 공통되는 상수이기 때문에 output $y$를 구하는데 전혀 영향을 주지 않는다. 그래서
\[y = \underset{c_k}{\text{argmax}} \; p(c_k) \cdot p(x \mid c_k)\]여기까지가 NB classifier에서 ‘Bayes’라는 이름이 붙는 이유다!
다음 단계는 $p(x \mid c_k)$를 raw한 데이터 $x$ 그대로 쓰는게 아니라 feature $(a_1, …, a_n)$의 형태로 기술하는 것이다. 우리는 메일 본문에서 몇가지 특징적인 부분들을 정할 수 있다. 'free'라는 단어의 유무, 'Call'라는 단어의 유무, 본문의 길이, 같은 단어가 최대 몇번 반복되는지 등등… Feature Extraction을 수행하면 raw text가 아니라 정량적인 feature의 형태로 데이터를 표현할 수 있다.
NB의 경우는 특정 단어가 등장 하는지 여부를 feature로 사용한다. 그래서 $p(w = \text{free} \mid S = T)$라고 하면… 스팸인 메일 중에서 $\text{free}$라는 단어가 등장할 확률을 말한다! 이것은
\[p(w = \text{free} \mid S = T) = \frac{\text{#. of spam mails contain word 'free'}}{\text{#. of spam mails}}\]로 쉽게 확률을 구할 수 있다! 👏
그래서 word $w_i$를 피처로 삼아 $p(x \mid c_k)$를 다시 적어보면 …
\[p(x \mid c_k) = p(a_1, ..., a_n \mid c_k)\]NB는 <naive assumption>이라는 가정을 한다. 이것은 아래와 같다.
“One assumption taken is the strong independence assumptions btw the features.”
즉, 각 피쳐가 서로 독립이다!를 가정한다. 이것은 곧 $p(a_1, …, a_n \mid c_k)$에 대해 아래가 성립함을 말한다.
\[p(a_1, ..., a_n \mid c_k) = p(a_1 \mid c_k) p(a_2 \mid c_k) \cdots p(a_n \mid c_k)\]그래서 각 피처의 확률을 단순히 곱하는 것만으로 joint probability $p(a_1, …, a_n \mid c_k)$를 구할 수 있다! 👍
물론 strong indepence 가정은 모델링을 위해 적당한 형태로 가정한 것일 뿐이다. 실제론 각 피처가 독립이 아니라 correlate 되어 있을 수 있다.
자! 그럼 원래 구하려고 했던 output $y$를 다시 구해보자.
\[y = \underset{c_k}{\text{argmax}} \; p(c_k) \cdot p(x \mid c_k)\]$p(x \mid c_k)$를 feature $a_i$의 형태로 바꾸고 <naive assumption>에 의해 위의 식은 아래가 된다.
\[\begin{aligned} y &= \underset{c_k}{\text{argmax}} \; p(c_k) \cdot p(a_1 \mid c_k) \cdots p(a_n \mid c_k) \\ &= \underset{c_k}{\text{argmax}} \; p(c_k) \cdot \prod_i^n p(a_i \mid c_k) \end{aligned}\]결국 각 레이블 $c_k$에 대해
- $S=T$에서의 $p(c_k) \cdot \prod_i^n p(a_i \mid c_k)$
- $S=F$에서의 $p(c_k) \cdot \prod_i^n p(a_i \mid c_k)$
값을 비교해 더 큰 레이블의 값을 output $y$로 매기면 되는 것이다! 🙌
구현
자… 그럼 이걸 코드로 구현해보자! 사실 구현 자체도 그리 어렵지 않으니 잘 따라와보자 😉
일단 스팸 데이터셋 SNS Spam Collection Dataset을 준비한다.
!wget https://raw.githubusercontent.com/mohitgupta-omg/Kaggle-SMS-Spam-Collection-Dataset-/master/spam.csv
그리고 적당히 데이터를 가공하고, train-test split을 수행하면…
data = pd.read_csv('spam.csv', encoding='latin1')
print("샘플 수", len(data)) # 5,572
data.head()
data = data[['v1', 'v2']] # 필요한 컬럼한 추출
data.head()
data['v1'] = data['v1'].replace(['ham','spam'],[0,1]) # label을 0, 1로 변경
data.head()
data_train, data_test = train_test_split(data, test_size=0.2, random_state=1)
X_train = data_train['v2']
y_train = data_train['v1']
X_test = data_test['v2']
y_test = data_test['v1']
print('=== 훈련 데이터 비율 ===')
print('ham', str(round(np.sum(y_train == 0) / len(y_train) * 100, 1)) + '%')
print('spam', str(round(np.sum(y_train == 1) / len(y_train) * 100, 1)) + '%')
print('=== 테스트 데이터 비율 ===')
print('ham', str(round(np.sum(y_test == 0) / len(y_test) * 100, 1)) + '%')
print('spam', str(round(np.sum(y_test == 1) / len(y_test) * 100, 1)) + '%')
...
=== 훈련 데이터 비율 ===
ham 86.4%
spam 13.6%
=== 테스트 데이터 비율 ===
ham 87.5%
spam 12.5%
메일 본문은 너무 raw한 데이터이기 때문에 바로 쓰기 보다는 전처리를 해주는게 좋다. HW5 과제에서 배운 토큰화(tokenization)을 활용해보자!
import nltk
from nltk.tokenize import sent_tokenize
nltk.download('punkt')
from nltk.tokenize import word_tokenize
from nltk.corpus import stopwords
nltk.download('stopwords')
stop_words = set(stopwords.words('english'))
def tokenize(text):
sentences = sent_tokenize(text)
tokens = []
for sentence in sentences:
# 단어 토큰화
words = word_tokenize(sentence)
for word in words:
word = word.lower() # 소문자 변환
if word in stop_words: continue # 불용어 제거
if len(word) <= 3: continue # 길이 3 이하 제거
tokens.append(word)
return tokens
텍스트에서 문장 토큰화와 단어 토큰화를 한 후, 불용어를 제거하고 길이 3 이하의 단어들을 모두 제거했다!
그리고 vocab = {}에 각 토큰의 빈도수를 저장하면 …
vocab = {}
for text in X_train:
# 토큰화
tokens = tokenize(text)
for token in tokens:
if token not in vocab:
vocab[token] = 0
vocab[token] += 1
print(vocab)
print(len(vocab))
...
{'sleeping': 10, 'feeling': 15, 'well': 86, 'come': 177, ...
7449
와 같이 출력 결과를 얻을 수 있다. 그런데 이 모든 토큰을 다 쓸 건 아니고 빈도수 Top 5의 단어에 대해서만 feature extraction을 적용할 것이다. 그래서 적당히 정렬해 target_token을 정하면…
# filter out top 5 tokens
vocab_sorted = sorted(vocab.items(), key=lambda x : x[1], reverse=True)
vocab_size = 5
vocab_sorted = vocab_sorted[:vocab_size]
print(vocab_sorted)
target_tokens = [word for word, _ in vocab_sorted]
print(target_tokens)
...
[('call', 460), ('know', 216), ('free', 212), ('like', 204), ('good', 193)]
['call', 'know', 'free', 'like', 'good']
위와 같이 5개의 단어가 추출되었다!
이제 이 5개 단어를 feature로 삼아서 확률 $p(a_i \mid S = T)$와 $p(a_i \mid S = F)$를 각각 구해보자.
# derive spam probability
X_train_spam = X_train[y_train == 1]
print('[train] # of spam', len(X_train_spam))
spam_count = {token: 0 for token in target_tokens}
for text in X_train_spam:
tokens = tokenize(text)
for target_token in target_tokens:
if target_token in tokens:
spam_count[target_token] += 1
print('spam count:', spam_count)
word_spam_prob = {token: spam_count[token] / len(X_train_spam) for token in spam_count}
print("P(w_i | S = T)", word_spam_prob) # P(w_i | S = T)
...
[train] # of spam 608
spam count: {'call': 263, 'know': 17, 'free': 132, 'like': 12, 'good': 10}
P(w_i | S = T) {'call': 0.43256578947368424, 'know': 0.027960526315789474, 'free': 0.21710526315789475, ...
ham의 경우도 비슷하게 구하면 된다.
이제 $p(c_k)$에 대응하는 $p(S = T)$, $p(S = F)$를 구해보자.
spam_prob = len(X_train_spam) / len(X_train)
ham_prob = 1 - spam_prob
print("spam_prob", spam_prob) # P(S = T)
print("ham_prob", ham_prob) # P(S = F)
이제 준비는 다 되었다! 미리 구한 확률값을 조합해 NB를 직접 구현해보자!
# apply naive bayes for train-set
correct_count = 0
for idx, text in X_train.items():
tokens = tokenize(text)
y_gt = y_train[idx]
# spam case
spam_prob_ = spam_prob
for token in tokens:
if token in target_tokens:
spam_prob_ *= word_spam_prob[token]
# ham case
ham_prob_ = ham_prob
for token in tokens:
if token in target_tokens:
ham_prob_ *= word_ham_prob[token]
y_pred = ham_prob_ < spam_prob_
correct_count += (y_gt == y_pred)
print(f'{round(correct_count / len(X_train) * 100, 1)}%')
...
89.7%
train-set에 적용했을 때, 89.7% 정도의 정확도를 보였다. 그러나 분류 문제는 단순히 정확도만으로는 성능이 좋다 나쁘다를 판단할 수 없다! 왜냐하면 현재의 train/test set에서 “어떤 메일이 입력되어도 ham으로 분류”하는 classifier도 ham의 비율이 압도적으로 많기 때문에 80% 이상의 정확도(accuracy)를 보이기 때문이다!
정확도(accuracy)의 이런 단순함 때문에 분류 문제에서는 정확도보다는 precision-recall 값을 기준으로 모델 성능을 판단한다.
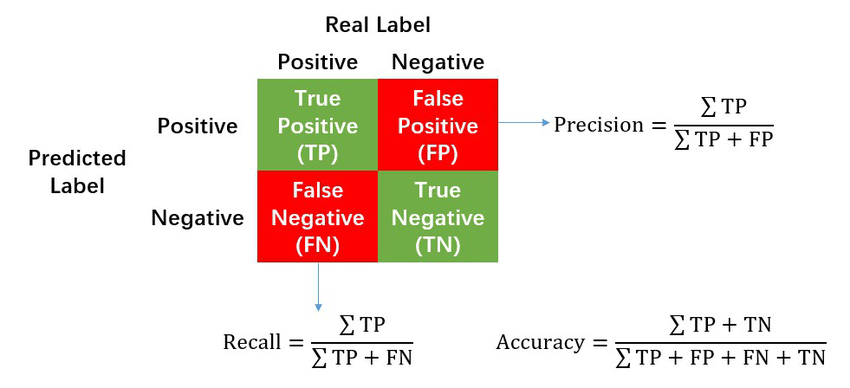
precision-recall 개념은 위의 2x2의 표로 전부 설명되는 개념이다.
- precision: positive라고 예측한 것중 실제로 positive가 있는 비율
- recall: 실제 positive인 것 중에서 제대로 맞춘 비율
소위 말하는 ‘좋은 모델’이 되려면 precision과 recall이 둘다 높은 값을 가져야 한다. 만약 위와 같이 “어떤 메일이 입력되어도 ham으로 분류”하는 classifier가 있다면, 그 classifier는
- 100개 샘플에 20:80 비율로 spam:ham이 분포함
- spam을 positive로 둔다 1
- 어떤 메일이 입력되어도 ham으로 분류: all predicted as negative(ham)
- precision: 모두 ham으로 분류하기 때문에 precision은 $0/0 = 0$
- recall: 제대로 분류한 spam이 없기 때문에 $0/20 = 0$
그래서 이 경우는 precision, recall 값이 0이기 때문에 좋은 모델이 아니라고 판단하며, 실제로도 ham으로만 분류하는 모델은 좋은 모델이 아니다 👊
어쨌든 전하고 싶은 내용은 정확도(accuracy) 뿐 아니라 precision, recall 값을 봐야 한다는 것이다! precision, recall 공식을 직접 구현해도 되겠지만, sklearn에 다 구현이 되어 있어서 가져다 쓰기만 하면 된다 😊
from sklearn import metrics
# apply naive bayes for train-set
correct_count = 0
y_preds = []
for idx, text in X_train.items():
tokens = tokenize(text)
y_gt = y_train[idx]
...
y_pred = ham_prob_ < spam_prob_
correct_count += (y_gt == y_pred)
y_preds.append(y_pred)
precision = metrics.precision_score(y_train.to_list(), y_preds)
recall = metrics.recall_score(y_train.to_list(), y_preds)
f1_score = metrics.f1_score(y_train.to_list(), y_preds)
print('precision:', round(precision, 3))
print('recall:', round(recall, 3))
print('f1_score:', round(f1_score, 3))
print(f'accuracy: {round(correct_count / len(X_train) * 100, 1)}%')
...
precision: 0.642
recall: 0.551
f1_score: 0.593
accuracy: 89.7%
출력된 값을 보면 정확도와는 값이 다르게 나오는 것을 볼 수 있다. 또, 0.5 수준이면 퍼포먼스가 좋은 편이 아니다 😢 또, f1_score라는 지표도 사용했는데, 공식은 아래와 같다.
대충 precision, recall을 종합한 지표 정도로 이해하면 된다. f1_score도 지표로 자주 사용하기 때문에 함께 알아두자!
precision, recall, f1_score 값을 보면 아직 0.5 수준으로 그렇게 높지 않다. 그래서 feature로 사용하는 단어의 수를 10개, 20개, 100개로 늘렸을 때 classifier의 성능이 어떻게 변하는지 살펴보자! vocab_size를 늘리기 편하게 코드를 함수화 하면 …
def generate_prob(X, y, vocab_size):
vocab_sorted = sorted(vocab.items(), key=lambda x : x[1], reverse=True)
vocab_sorted = vocab_sorted[:vocab_size]
target_tokens = [word for word, _ in vocab_sorted]
# derive spam probability
X_spam = X[y == 1].copy()
spam_count = {token: 0 for token in target_tokens}
for text in X_spam:
tokens = tokenize(text)
tokens = set(tokens)
for target_token in target_tokens:
if target_token in tokens:
spam_count[target_token] += 1
word_spam_prob = {token: spam_count[token] / len(X_spam) for token in spam_count}
X_ham = X[y == 0]
ham_count = {token: 0 for token in target_tokens}
for text in X_ham:
tokens = tokenize(text)
tokens = set(tokens)
for target_token in target_tokens:
if target_token in tokens:
ham_count[target_token] += 1
word_ham_prob = {token: ham_count[token] / len(X_ham) for token in ham_count}
return word_spam_prob, word_ham_prob
def evaludate_classifier(X, y, vocab_size=5):
word_spam_prob, word_ham_prod = generate_prob(X, y, vocab_size)
correct_count = 0
y_preds = []
for idx, text in X.items():
tokens = tokenize(text)
y_gt = y[idx]
# spam case
spam_prob_ = np.log(spam_prob) # handle unserflow
for token in tokens:
if token in word_spam_prob and word_spam_prob[token] != 0:
spam_prob_ += np.log(word_spam_prob[token])
# ham case
ham_prob_ = np.log(ham_prob)
for token in tokens:
if token in word_ham_prob and word_ham_prob[token] != 0:
ham_prob_ += np.log(word_ham_prob[token])
y_pred = ham_prob_ < spam_prob_
correct_count += (y_gt == y_pred)
y_preds.append(y_pred)
accuracy = correct_count / len(X)
precision = metrics.precision_score(y.to_list(), y_preds)
recall = metrics.recall_score(y.to_list(), y_preds)
f1_score = metrics.f1_score(y.to_list(), y_preds)
return (accuracy, precision, recall, f1_score)
이때, evaludate_classifier()에서 spam_prob_와 ham_prob_를 구하는 부분이 학률을 곱하는 것 대신 np.log() 값을 더하는 것으로 바뀌었다. 이것은 확률 곱셈이 계속되어서 언더 플로우가 발생하는 걸 처리하기 위해서 수정한 것이다!
이제 위의 코드로 vocab_size 1부터 150까지의 모델 성능은 아래와 같다.
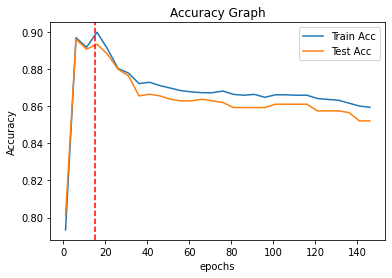
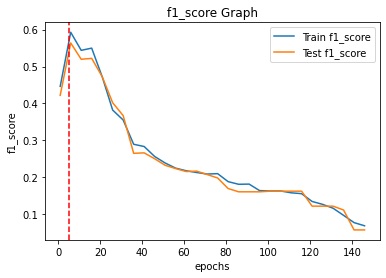
결과를 보면 vocab_size=20까지는 피처를 늘리는 것이 모델 성능 향상에 도움이 되지만, 그 이후부터는 성능이 낮아지는 걸 볼 수 있다.
맺음말
이번 포스트에서는 자연어 데이터를 전처리하고, 그걸 학습 데이터로 쓰는 Naive Bayes Classifier를 구현해보았다. NB Classifier가 딥러닝 모델은 아니지만, 워낙 유명한 모델이기 때문에 한번쯤 직접 구현해보는 걸 추천한다.
다음 세미나에서는 딥러닝 모델 중 하나인 RNN, LSTM을 살펴보고, 이를 활용한 모델을 직접 구현해보겠다!
-
ham을 positive라고 둘 수도 있겠지만, 보통 그 수가 더 적은 레이블을 positive로 설정하거나 detect 해야만 하는 것을 positive로 설정한다. 지금은 spam detection을 다루지만, 악성 종양을 다루는 경우라면 양성(Benign)과 악성(Malignant) 중 악성인 경우를 positive로 설정한다. ↩